- Bernard Kolman
- Poole David
- Nakos George, Joyner David
- Proskuriakov, I Problemario
- Heinhold, Joseph, Bruno Reidmuller Determinantes y sistemas de ecuaciones
- Julia García Cabello
- Gilbert Strang
- Manuel Iglesias Cerezal problemas
- Ángel Balaguer Beser,Elena Alemany Martínez
domingo, 29 de noviembre de 2009
Bibliografia
lunes, 23 de noviembre de 2009
Producto Interior
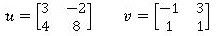
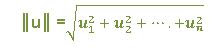
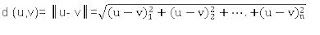
Ejemplo
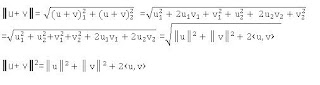
Rango y Nulidad de una Matriz

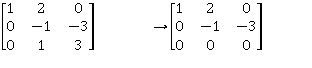

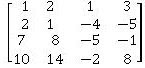
a | b | c | d | e | f | g | |
Tamaño de A | 3x3 | 3x3 | 3x3 | 5x9 | 9x5 | 4x4 | 6x2 |
Rgo A | 3 | 2 | 1 | 2 | 2 | 0 | 2 |
viernes, 20 de noviembre de 2009
Base y Dimensión
Si V es cualquier espacio vectorial y S ={v1 ,v2,…….vn} es un conjunto de vectores en V, entonces S se llama base de V si se cumplen las siguientes condiciones:
- S es linealmente independiente
- S genera V
Ejemplo
El conjunto S={ v1,v2,v3,v4}, donde v1=(1,0,1,0),v2=(o,1,-1,2),v3=(0,2,2,1), V4=(1,0,0,1) es una base para R4
En primer lugar hay que demostrar que es linealmente independiente,
Resolver el determinante factible si la matriz generada posee una dimensión que lo permita, es decir menos cálculo que por otro método. La matriz generada siempre es cuadrada sino no sería base

Se realiza la eliminación guassiana –f1 +f4~f4
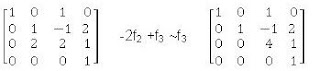
Se ha triangulado la matriz por lo tanto forman base.
La dimensión de un espacio vectorial no nulo es el número de vectores en una base V. Se simboliza dim V
Ejemplo
- La dimensión de R2 es 2, la dimensión de R3 es tres.
En el ejemplo de base se puede decir que dim V = 4
Espacio vectorial
- Independencia Lineal.
Los vectores v1, v2, …..vn de un espacio vectorial son linealmente dependientes si existen constantes c1, c2,……..cn no todas iguales a cero que satisfagan la siguiente expresión (son dependientes si aparte del cero hay otras respuestas, se recuerda que el sistema de ecuaciones generado en esta ocasión es homogéneo):
Ejemplo:
- Determinar si los vectores (-1,1,0,0) y (-2,0,1,1) son linealmente independientes entre si.
Otro método para resolver este tipo de ejercicios es el siguiente:
Cada vector es una fila de una matriz a la cual se le escalonará por eliminación gaussiana. Retomando el ejemplo anterior
Se puede llegar a la conclusión que son linealmente independientes, ya que se pudo escalonar la matriz. De caso contrario que una de las filas de la matriz se anulara la conclusión sería dependencia lineal.
- Considerando los vectores
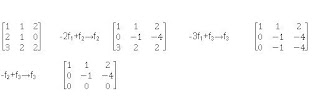
Como se anuló la tercera fila esto indica dependencia lineal entre los vectores.
Nota: este espacio vectorial se refiere a polinomios de segundo orden, donde se deben agrupar por el grado, es decir lineales con lineales, independientes con independientes y los elementos que no encuentran presentes se les deben colocar cero (0).
Podran encontrar mas ejercicios en el siguiente enlace.
Algebra lineal Bernard Kolman pág 301
miércoles, 18 de noviembre de 2009
Transformación Lineal
Definición
Si T: V→W es una función de un espacio vectorial V a un espacio vectorial W, entonces T se llama transformación lineal de V a W, si para todos los valores u y v y los escalares c, se define que
- T(u+v)=Tu+Tv
- T(cu)= cTu
En casos especiales T: V→V es decir el mismo espacio vectorialse llama operador lineal.
Propiedades
Si T: V→W
- T(0)=0
- T(-v)= -T(v)
- T(u-v)= T(u)-T(v)
Por medio de la definición de transformación lineal
1.- Sea V=(-∞,∞) el espacio vectorial de funciones de primera derivada continuas sobre (-∞,∞) y W= F(-∞,∞) el espacio vectorial de todas las funciones con valores reales definidas sobre (-∞,∞)
T: V→W
D(f) = fx'
T(f+g)= Tf +Tg(fx+gx)'= (fx)' +(gx)'
Esto se cumple
T(cf)= cT(fx)(cfx)'=c(fx)'
2.- Si T: Mnn→R
T(A)= A
- T(A+B)≠ T(A)+T(B)
- TcA ≠ cTA
1.-Si T: Mnn→R
T(A)= tr A
2.- Si V→R donde V es un espacio con producto interior y Tu = ║u║.
Mas ejercicios
Espacio Vectorial
Combinación Lineal
Un vector w se denomina combinación lineal de los vectores v1, v2,……….vn
Si se puede expresar de la forma
kn son escalares.
Este conjunto de vectores se denota como
, v2 ,v3 …. vn }
1.-Todo vector v={a, b, c } en R3 se puede expresar como una combinación de los vectores estándar básicos
i=(1,0,0) , j=(0,1,0) , k=(0,0,1)
v= (a, b, c) = a (1,0,0) + b (0,1,0) + c (0,0,1) = ai + bj +ck
2.- Considerar los vectores u=(1,2,-1), y v=(6,4,2) en R3. Demostrar que w=(9,2,7) es una combinación lineal de u y v, y que w=(4,-1,8) no lo es.
Hay que encontrar los escalares que satisfacen la ecuación siguiente:
W= k1 u + k2 v
(9,2,7)= k1 (1,2,-1) + k2 (6,4,2)
(9,2,7)= (1 k1, 2 k1,-1k1) + (6 k2 ,4 k2 ,2 k2 )
Igualando
9= k1 +6k2
2= 2k1 +4k2
7 = -k1 +2k2
Resolviendo el sistema k1 = -3 k2 = 2
La respuesta es:
(4,-1,8)= k1 (1,2,-1) + k2 (6,4,2)(4,-1,8)= (1 k1, 2 k1,-1k1) + (6 k2 ,4 k2 ,2 k2 )
Igualando
4= k1 +6k2
-1= 2k1 +4k2
8= -k1 +2k2
Resolviendo el sistema se llega a la conclusión que es inconsistente, por lo tanto no es combinación lineal.
1.-Determinar si el vector v pertenece a gen = { v1 v2,v3} donde
V1=(1,0.0,1) v2=(1,-1,0.0) v3=(0,1,2,2)
- V=(-1,4,2,2)
- V =(1,2,01)
- V=(-1,1,4,3)
- V=(0.1.10)


domingo, 15 de noviembre de 2009
Espacio Vectorial y sub espacio
Espacio Vectorial
Un espacio vectorial real es un conjunto de V con dos operaciones básicas adición entre vectores y multiplicación por un escalar que satisfacen las siguientes axiomas:
- Si u y v son elementos cualquiera en V, entonces u + v pertenece a V Ley de cerradura
- u + v = v + u
Ley conmutativa
- u + (v + w) = (u + v) + w
Ley Asociativa
- Existe un elemento 0 en tal u
que u + 0 = 0 + u = u, para todo valor de u. Elemento Neutro para la suma - Para cada u en V existe un elemento – u en V t al que u + (-u)=0
Elemento Simétrico o Negativo
- Si u es cualquier elemento de V y c es cualquier número real, entonces c.u pertenece a V Ley de cerradura
- c (u + v) = cu + cv , para todo
real c y todo elemento u y v en V. Ley Distributiva
- (c+d) u = cu + du
para todo número real c y d
y todo elemento u en V.
Ley Distributiva
- c.(du) = (cd) u para todo número real c y d
y todo elemento u en V. Ley asociativa de la multiplicación
- 1u =u, para u en V.
Ejemplos:
- Considerando el conjunto V de todas las tercia ordenadas de números reales de la forma (x, y, 0) y se define las operaciones como
(X, y,0) + (x', y',0'') = ( x +x , y + y, 0)
c(x,y,0) = (cx, cy 0)
Comprobando cada axioma:
- Se cumple el primer axioma puesto que dada la operación la forma se mantiene, lo que implica que pertenece a V
(X, y,0) + (x', y',0'') = ( x +x , y + y, 0)
- (X, y,0) + (x', y',0'') = (x'' ,y',0) + (x, y, 0)
( x +x , y + y, 0) = (x' +x, y'+y, 0)
- {(X, y,0) + (x', y',0'')} + (x2, y2, 0) = (X, y,0) +{ (x', y',0'') + (x2, y2, 0)}
(x +x , y + y, 0) + (x2,y2,0)= (X, y,0) + (x'+x2, y'+y2 , 0 )
(x+x'+x2, y+y'+y2, 0) =(x+x'+x2, y+y'+y2, 0)
- (X, y,0) + (0,0,0') = ( x , y, 0)
- (X, y,0) - (x,y,0'') = ( 0 ,0, 0)
- Se cumple el sexto axioma puesto que dada la operación la forma se mantiene, lo que implica que pertenece a V
c(x,y,0) = (cx, cy 0)
- c{(X, y,0) + (x', y',0'')} = c(x,y,0) + c(x',y',0)
c( x +x , y + y, 0) = (cx, cy, 0) + (cx' , cy', 0)
(c[x+x'], c[y+y'], 0)= (cx+cx', cy+cy' ,0)
- (c+d) (x,y,0) = c(x, y, 0) + d(x, y,0)
{(c+d) x, (c+d)y , 0) = (cx+dx , cy+dy ,0)
- (cd) (x,y,0) = c( d(x, y,0))
{(cd) x, (cd)y , 0) = (cdx , cdy ,0)
- 1(x,y,0) = (x, y, 0)
En conclusión es un espacio vectorial puesto que cumple los 10 axiomas
- Considerando el conjunto V de todas las tercia ordenadas de números reales de la forma (x, y, 0) y se define las operaciones como
(X, y,z) + (x', y',z'') = ( x +x , y + y, z+z)
c(x,y,z) = (cx, y z)
Es fácil comprobar los primeros axiomas puesto que cumplen las propiedades de los números,
Comenzar por el axioma 7
- c{(X, y,z) + (x', y',z'')} = c(x,y,z) + c(x',y',z')
c( x +x' , y + y', z+z') = (cx, y, z) + (cx' , y', z')
(c[x+x'], [y+y'], [z+z'[)= (cx+cx', y+y' ,z+z')
- (c+d) (x,y,z) ≠ c(x, y, z) + d(x, y,z)
{(c+d) x, y , z)} ≠ (cx+dx , y+y , z+z)
{(c+d) x, y , z)} ≠ (cx+dx , 2 y ,2z)
no se cumple este axioma
Ejercicios.
Algebra lineal una introduccion moderna David Poole pag 445
Sub espacio Vectorial
Sea un espacio vectorial V y W un subconjunto no vacio de V. Si W es un espacio vectorial con respecto de las operaciones en V, entonces W es un sub espacio vectorial.
- Si u y v son elementos cualquiera en V, entonces u + v pertenece a V Ley de cerradura
- Si u es cualquier elemento de V y c es cualquier número real, entonces c.u pertenece a V Ley de cerradura
Ejemplo
Cuál de los siguientes
subconjuntos de
R son sub espacios de R. El conjunto de la forma:
- (a,b,2)
- (a,b,c) donde c= a+b
a (a,b,2) + (a1,b1,2) = (a+a, b+b, 2+2)
no cumple con la forma por lo tanto no es sub espacio vectorial
b ./ (a b, c) + (a1,b1,c) = (a+a1, b+b1, c+c1)
c= a + b y c1= a1+b1
c+ c1 = (a+a1)+ (b+b1)i se cumple
K(a,b,c) = (Ka, Kb, kc)
C= a+b y k c = ka +k b también se cumple.
lunes, 2 de noviembre de 2009
Ejercicios de Espacio Vectorial
1.-Sea (x,y,z) en R3
(x, y, z) + (x’,y’,z’) = (x’,y+y’,z’)
C(x, y, z) = (cx, cy, cz)
2.- Sea (x,y,z) en R3
(x, y, z) + (x’,y’,z’) = (x+x’,y+y’,z+z’)
C(x, y, z) = (x, 1, z)
3.- El conjunto de los números reales positivos u con operaciones u+v = u.v
Y cu = uc
4.- El conjunto de los números reales definidos por operaciones
u+v = 2 u-v y cu = cu
5.- El conjunto de todos los pares ordenados de números reales (x,y) con adición en R2 y la multiplicación por un escalar a(x,y) = (x, y)
6.- El conjunto de todos los pares ordenados de números reales (x,y) con las operaciones
(x, y) + (x’,y’) = (x+x’,y+y’)
C(x, y,) = (0, 0)
7.-V es el conjunto de todos los polinomios de la forma at2+ bt +c, donde a, b y c son números reales con b=a+1
(at2 + bt +c) + (a1 t2+ b1 t +c1) = (a+a1) t2 + (b+b1) t+ (c+c1)
r (at2 + bt +c)= rat2+ rbt + rc
8.- El conjunto V de todas las matrices 2x2, la adición usual M22 y la multiplicación por un escalar definida por cA=c AT.
tipos de matrices
| Tipo de matriz | Definición | Ejemplo |
| VECTOR FILA | Aquella matriz que tiene una sola fila, siendo su orden 1×n | |
| VECTOR COLUMNA | Aquella matriz que tiene una sola columna, siendo su orden m×1 | |
| RECTANGULAR | Aquella matriz que tiene distinto número de filas que de columnas, siendo su orden m×n , | |
| TRASPUESTA | Dada una matriz A, se llama traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.
| |
| OPUESTA | La matriz opuesta de una dada es la que resulta de sustituir cada elemento por su opuesto. La opuesta de A es -A. | |
| NULA | Si todos sus elementos son cero. También se denomina matriz cero y se denota por 0m×n | |
| CUADRADA | Aquella matriz que tiene igual número de filas que de columnas, m = n, diciéndose que la matriz es de orden n.
| |
| SIMÉTRICA | Es una matriz cuadrada que es igual a su traspuesta.
| |
| ANTISIMÉTRICA | Es una matriz cuadrada que es igual a la opuesta de su traspuesta.
| |
| DIAGONAL | Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal | |
| ESCALAR | Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal que son iguales | |
| IDENTIDAD | Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal que son iguales a 1. También se denomina matriz unidad. | |
| TRIANGULAR | Es una matriz cuadrada que tiene todos los elementos por encima (por debajo) de la diagonal principal nulos. | |
| ORTOGONAL | Una matriz ortogonal es necesariamente cuadrada e invertible: A-1 = AT
| |
| NORMAL | Una matriz es normal si conmuta con su traspuesta. Las matrices simétricas, antisimétricas u ortogonales son necesariamente normales. | |
| INVERSA
| Decimos que una matriz cuadrada A tiene inversa, A-1, si se verifica que :
|
|























