Base y Dimensión

Espacio Vectorial

Base y Dimensión



Si V es cualquier espacio vectorial y S ={v₁ ,v₂,…….v_n} es un conjunto de vectores en V, entonces S se llama base de V si se cumplen las siguientes condiciones:

1. S es linealmente independiente
   
2. S genera V
   

Reciben el nombre de base natural o canónica

Ejemplo

El conjunto S={ v₁,v₂,v₃,v₄}, donde v₁=(1,0,1,0),v₂=(o,1,-1,2),v₃=(0,2,2,1), V₄=(1,0,0,1) es una base para R⁴



En primer lugar hay que demostrar que es linealmente independiente,

C₁ v₁ +c₂ v₂ + c₃ v₃ + c₄ v₄ =0

Se puede efectuar como se realizó para independencia lineal construyendo la matriz. Es válido, además resolver el determinante puesto que una de las condiciones para formar la base es el número de vectores que la forman. Si el determinante es distinto de cero (0) se dice que es independiente lineal por lo tanto forman la base, mientras que el resultado si es igual a cero no forman base. (Recordar las propiedades de los determinantes)

Resolver el determinante factible si la matriz generada posee una dimensión que lo permita, es decir menos cálculo que por otro método. La matriz generada siempre es cuadrada sino no sería base



Se realiza la eliminación guassiana –f₁ +f₄~f₄



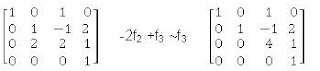
Se ha triangulado la matriz por lo tanto forman base.



La dimensión de un espacio vectorial no nulo es el número de vectores en una base V. Se simboliza dim V



Ejemplo

1. La dimensión de R² es 2, la dimensión de R³ es tres.
   
2. 
   
   En el ejemplo de base se puede decir que dim V = 4