Espacio vectorial
- Independencia Lineal.
Los vectores v1, v2, …..vn de un espacio vectorial son linealmente dependientes si existen constantes c1, c2,……..cn no todas iguales a cero que satisfagan la siguiente expresión (son dependientes si aparte del cero hay otras respuestas, se recuerda que el sistema de ecuaciones generado en esta ocasión es homogéneo):
C1 v1 + c 2v2+……cn vn =0
En caso contrario se dice que v1, v2, …..vn son linealmente independientes. Es decir que se debe cumplir la ecuación anterior y los valores de c1 = c2=…….=.cn=0. La única posibilidad de combinación lineal de ellos es que sean iguales a cero. Ejemplo:
- Determinar si los vectores (-1,1,0,0) y (-2,0,1,1) son linealmente independientes entre si.
C1 (-1,1,0,0) + c2 (-2,0,1,1)=(0,0,0,0)
-c1 -2c2 =0
C1+ 0c2 =0
C2=0
C2=0
La única solución de este sistema es c1 = c2=0 Otro método para resolver este tipo de ejercicios es el siguiente:
Cada vector es una fila de una matriz a la cual se le escalonará por eliminación gaussiana. Retomando el ejemplo anterior
-2f1 +f2 → f2
Se puede llegar a la conclusión que son linealmente independientes, ya que se pudo escalonar la matriz. De caso contrario que una de las filas de la matriz se anulara la conclusión sería dependencia lineal.
- Considerando los vectores
p1 (t)= t2 + t + 2 p2 (t)= 2t2 + t p3 (t)= 3t2 + 2t + 2
son linealmente independientes o no
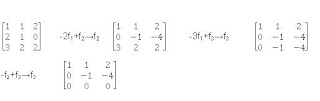
Como se anuló la tercera fila esto indica dependencia lineal entre los vectores.
Nota: este espacio vectorial se refiere a polinomios de segundo orden, donde se deben agrupar por el grado, es decir lineales con lineales, independientes con independientes y los elementos que no encuentran presentes se les deben colocar cero (0).
Podran encontrar mas ejercicios en el siguiente enlace.
Algebra lineal Bernard Kolman pág 301


No hay comentarios:
Publicar un comentario