Espacio Vectorial
Si V es cualquier espacio vectorial y S ={v1 ,v2,…….vn} es un conjunto de vectores en V, entonces S se llama base de V si se cumplen las siguientes condiciones:
- S es linealmente independiente
- S genera V
Ejemplo:
El conjunto S={ v1,v2,v3,v4}, donde v1=(1,0,1,0),v2=(o,1,-1,2),v3=(0,2,2,1), V4=(1,0,0,1) es una base para R4
En primer lugar, hay que demostrar que es linealmente independiente,
C1 v1 +c2 v2 + c3 v3 + c4 v4 =0
Se puede efectuar como se realizó para independencia lineal construyendo la matriz. Es válido, además, resolver el determinante puesto que una de las condiciones para formar la base es el número de vectores que la forman. Si el determinante es distinto de cero (0) se dice que es independiente lineal, por lo tanto, forman la base, mientras que el resultado si es igual a cero no forman base. (Recordar las propiedades de los determinantes)Resolver el determinante factible si la matriz generada posee una dimensión que lo permita, es decir, menos cálculo que por otro método. La matriz generada siempre es cuadrada si no no sería base
Se realiza la eliminación gaussiana –f1 +f4~f4
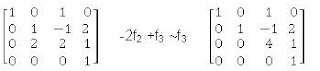
Se ha triangulado la matriz, por lo tanto, forman base.
La dimensión de un espacio vectorial no nulo es el número de vectores en una base V. Se simboliza dim V
Ejemplo
En el ejemplo de base se puede decir que dim V = 4
Rango y nulidad
La dimensión común del espacio renglón y del espacio columna de una matriz A se denomina rango y se denota rango (A), la dimensión del espacio nulo de A se llama nulidad y se denota nulidad (A).
Propiedad
Rango (A)= Rango (AT)
Teorema de la dimensión
Si es una matriz A con n columnas, entonces:
Rango (A) + nulidad (A) = n
El procedimiento para calcular el rango de una matriz es el siguiente Se utiliza los procesos elementales por filas para transformar A en una matriz B en forma escalonada.
El Rango de A es igual al número de filas no nulas (aquellas que se lograron escalonar).
Ejemplo
Sea A. determinar su rango y nulidad
Por procesos elementales
–f1+f2→f2 ^ –f1+f3→f3 f2+f3→f3
Ejercicios
Calcule el rango y la nulidad de A
En cada caso usa la información que proporciona la tabla para encontrar la nulidad de A y AT
a | b | c | d | e | f | g | |
Tamaño de A | 3x3 | 3x3 | 3x3 | 5x9 | 9x5 | 4x4 | 6x2 |
Rgo A | 3 | 2 | 1 | 2 | 2 | 0 | 2 |
