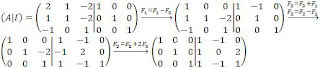Algebra de matrices

Álgebra de Matrices

1.- Suma de Matrices

      Dadas dos matrices de la mismo orden, A=(a_ij) y B=(b_ij), se define la matriz suma como: A+B=(a_ij+b_ij). Es decir, aquella matriz cuyos elementos se obtienen: sumando los elementos de las dos matrices que ocupan la misma posición.

 Propiedades de la suma de matrices

• Interna:

La suma de dos matrices de orden m x n es otra matriz dimensión m x n.

• Asociativa:

A + (B + C) = (A + B) + C

• Elemento neutro:

A + 0 = A

Donde O es la matriz nula de la misma dimensión que la matriz A.

• Elemento opuesto:

A + (-A) = O 

La matriz opuesta es aquella en que todos los elementos están cambiados de signo.

• Conmutativa:

A + B = B + A

Video de explicación de esta operación

2.- Matriz Traspuesta

     Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas

Propiedades

1. (A^T)^T = A    
2. (A + B)(A+B)^T = A = A^T + B^T
3. (k ·A)^T = k· A^T
4. (A · B)^T = B^T · A^T

3.- Producto de un escalar por una matriz

   Dada una matriz A=(a_ij) y un número real kR, se define el producto de un número real por una matriz: a la matriz del mismo orden que A, en la que cada elemento está multiplicado por k.

kA=(k a_ij)

  Propiedades 

•           Asociativa

a · (b · A) = (a · b) · A A M_mxn, a, b son constantes

• Distributiva

a · (A+B) = a · A + a · B A,B M_mxn , a

(a+b) · A = a · A+b · A A M_mxn , a, b

• Elemento Neutro

1 · A = A A M_mxn

• Traspuesta

(aA)^t = a A^t

Video de explicación

Video 2

 

4.- Producto de matrices

        Dos matrices A y B se dicen multiplicables si el número de columnas de A coincide con el número de filas de B.

M_{m x n} x M_{n x p} = M _{m x p}

       El elemento c_ij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos.

 

  Propiedades del producto de matrices

• Asociativa:

A · (B · C) = (A · B) · C

• Elemento neutro:

A · I = A

Donde I es la matriz identidad del mismo orden que la matriz A.

• No es Conmutativa:

A · B ≠ B · A

• Distributiva del producto respecto de la suma:

A · (B + C) = A · B + A · C

5.-Matriz inversa

 una matriz cuadrada A tiene inversa, A-1, si se verifica que : 

       Es aquella matriz cuadrada si se verifica que A·A^-1 = A^-1·A = I  está se puede obtener  por  los procesos elementales aplicados a una matriz identidad, como se muestra a continuación:

[A : I]  (matriz ampliada)

Procesos elementales a la matriz 

[I :A^-1]

Propiedades

1. (A · B)^-1 = B^-1 · A^-1
2. (A^-1)^-1 = A
3. (k · A)^-1 = k^-1 · A^-1
4. (A ^t)^-1 = (A ^-1)^t 
5. A · A^-1 = A^-1 · A = I

Video de explicación

Cálculo por el método de Gauss

    Sea A una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos como A^-1, seguiremos los siguientes pasos: 

[A : I]
      → Procesos elementales
[I: A^-1]

1º Construir una matriz del tipo M = (A I), es decir, A está en la mitad izquierda de M y la matriz identidad I en la derecha.

Considerando una matriz 3x3 arbitraria

2º  Utilizando el método Gauss se transforma la mitad izquierda, A, en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa: A^-1.Se inicia el proceso con el 1 pibot que permite encontrar los ceros necesarios.

 Otro ejemplo

Video de explicación

 

Forma matricial de un sistema lineal de ecuaciones

Un sistema lineal de m ecuaciones con n incógnitas es un sistema de la forma

Donde:

A=
es la matriz de coeficientes del sistema.
X= es la matriz de incógnitas. B= es la matriz de términos independientes.
Luego un sistema lineal de ecuaciones se puede expresar matricialmente como A·X=B
Si la matriz de coeficientes es invertible, es decir, posee inversa entonces el sistema tiene solución

A·X=B 

A^-1·A·X=A^-1·B 

              X=A^-1·B·. 

Por tanto resolver un sistema de ecuaciones a través de matrices consiste en poner el sistema en forma matricial. La solución, si la hay, será el producto de la inversa de la matriz de coeficiente (A^-1) por la matriz de términos independientes (B)

Ejercicios

Encontrar la inversa de las siguientes matrices

Si

Despeje x de Ax=b si

6.-Traza de una Matriz

La traza de una matriz cuadrada A de n x n está definida como la suma de los elementos de la diagonal principal de A.

Es decir,

donde aij representa el elemento que está en la fila i ésima y en la columna j ésima de A

Propiedades

• tr (A+B)=tr A +tr B
• tr (rA) =rtr (A)
• tr ( A^T)= tr (A)
• tr (AB)= tr(A) tr(B)
  

7.- Potencia de Matrices

Consiste en multiplicar tantas veces la matriz como lo indica el exponente.

A = ( 1 -2 ) 5 3

A . A = A2 = ( -9 -8 ) 20 -1

Propiedades

 Ejercicios

Realizar  las siguientes operaciones

 

Calcular las siguientes matrices de ser posible:

3A-2B

B+D

2B-2E

5C

4A^t-3C

A-D

3E^T

(A+C)^T