Producto Interior
Un producto interior sobre un espacio vectorial V es una función que asocia un número real ‹u, v› a cada pareja de vectores u y en V de forma que los siguientes axiomas se cumplen para los vectores u, v y w en V los escalares k.
‹u, v› = ‹v, u› Axioma de la simetría
2. ‹u+ v, w › = ‹u, w› + ‹ v, w› Axioma de aditividad
3. ‹ku, v›=‹u, kv › = k ‹u, v› Axioma de la homogeneidad
4. ‹u, u› ≥ 0 donde ‹u, u› = 0 si y sólo si u=0 Axioma de positividad
Fórmula
u= (u1 ,u2,….un) y v=(v1 ,v2,……,vn)
‹u, v›= u1 v1 +u2 v2+…..+un vn
Ejemplo
U=(1,2) V=(0,3)
‹u, v›= 1*0+2*3=0+6=6
Ejercicios
1.- Sea ‹u, v› el producto interior sobre R y u=(3,-2), v=(4,5) y w=(-1,6)
K=4
Encontrar
a) ‹u, v›=‹v, u› b) ‹u+ v, w › = ‹u, w› + ‹ v, w› c) ‹k u, v›=‹u, k v › = k ‹u, v›
2.- Calcular ‹u, v›
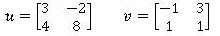
Propiedades del producto interior
1.- ‹0, v› = ‹v, 0›=0
2.- ‹u+ v, w › = ‹u, w› + ‹ v, w›
3.- ‹k u, v›=‹u, k v› = k ‹u, v›
4.- ‹u- v, w › = ‹u, w› - ‹ v, w›
5.- ‹u, v- w › = ‹u, v› + ‹u, w›
Norma de un vector
Si v es un espacio vectorial con producto interior, entonces la norma (o longitud) de un vector ║u║ en V se denota por y y se define como:
u= (u1 ,u2,….un)
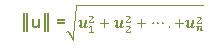
Comparando las fórmulas
‹u, v›= u1 v1 +u2 v2+…..+un vn
Se puede concluir que
║u║=‹u, u›1/2
Ejemplo
U=(1,2)
Si u y v son vectores en un espacio en V y k un escalar
1.- ║u║≥0
2.- ║u║= 0 si y solo si u=0
3. -║k u║ = 1k1 ║u║
4.- ║u+ v║≤║u║+║v║ desigualdad del triángulo
Distancia entre dos vectores
Se define como
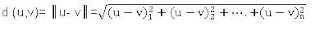
Ejemplo
U=(1,2) V=(0,3)
Propiedades
1.- d (u,v)≥0
2.- d (u,v)= 0 si y solo si u=v
3.- d (u,v)= d (v,u)
De acuerdo a lo antes expuesto
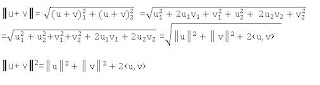
Ejercicios
1.- Hallar el valor de la norma de los siguientes vectores
2.- Hallar la distancia entre los vectores
U=(-1,3) v=(3,0)
P=3+3x q= 2+4x-x2
3.- Suponer que u, v y w son vectores tales que;
‹u, v›=2 ‹u, w›= 5 ‹w, v›= -3 ║u║= 1 ║v║=2 ║w║=7
Hallar
‹u+ v, v + w› ‹2v-w, v-u›
║u+ v║ ║2w- v║ ║2u+ v-w║Desigualdad de Cauchy Schwarz
Si u y v son dos vectores diferentes de cero en R ó R y es el ángulo entre estos vectores:
Desigualdad de Cauchy Schwarz
u.v≤║u║║v║
Hallar el coseno del ánguloU=(1,9) v=(7.5)
P=2+3x-2x2 q=5-x

Comprobar la desigualdad de Cauchy Schwarz con los vectores anteriores.
cos
|
ángulo
| |
0
|
90°
|
u.v
|
1
|
0° ó 360°
|
u.v=║u║║v║
|
-1
|
180°
|
u.v=║u║║v║
Son de igual módulo por el producto interior es negativo
|
Es una base normal cuando la norma de los vectores que la conforman es iguales a 1
Base Ortogonal
Es una base ortogonal cuando el producto interior de los vectores que la conforman es iguales a 0. De acuerdo a la tabla anterior se puede deducir que hay un ángulo recto entre los vectores que forman la base.
Base ortonormal
Es aquella que reúne las dos condiciones.
1.- Cuál de los siguientes conjuntos de vectores son ortonormales
(-1,2) (6,3)
(1,0,-1)(2,0,2)(0.5,0)

Normalización
Esto proceso consiste en transformar las normas en 1. Selogra dividiendo el vector entre su norma

Ejemplo
U=(-1,2)

No es normal hay que efectuar el procedimiento

Proceso de Ortonormalización de Gram Schmidt
El objetivo de este proceso es orgonalizar y normalizar los vectores de una base según este esquema
Se parte de un de conjunto de vectores {u1 ,u2 ,….un }
- Sea v1 =u1
- hay que normalizar


4.- hay que normalizar

5.-

6.- hay que normalizar

S={v1, v2, v….vn} esta es la nueva base ortonormal, el proceso es repetitivo tantas veces como vectores se tenga que ortonormalizar.
Ejemplo

Usando el proceso de Gram Schmidt, transformar la base en ortonormal
1.- (1,-3) (2,2)
2.- (1,1,1),(-1,12),(1,2,1)
3.- ( (0,2,1,0),(1-1,0,0),(1,2,0,-1),(1,0,0,1)
Mas ejercicios





