Producto Interior

Producto Interior

Un producto interior sobre un espacio vectorial V es una función que asocia un número real ‹u, v› a cada pareja de vectores u y en V de forma que los siguientes axiomas se cumplen para los vectores u, v y w en V los escalares k.

‹u, v› = ‹v, u› Axioma de la simetría

2. ‹u+ v, w › = ‹u, w› + ‹ v, w› Axioma de aditividad

3. ‹ku, v›=‹u, kv › = k ‹u, v› Axioma de la homogeneidad

4. ‹u, u› ≥ 0 donde ‹u, u› = 0 si y sólo si u=0 Axioma de positividad

Fórmula

u= (u₁ ,u₂,….u_n) y v=(v₁ ,v₂,……,v_n)

‹u, v›= u₁ v₁ +u₂ v₂+…..+u_n v_n

Ejemplo

U=(1,2) V=(0,3)

‹u, v›= 1*0+2*3=0+6=6

Ejercicios

1.- Sea ‹u, v› el producto interior sobre R y u=(3,-2), v=(4,5) y w=(-1,6)

K=4

Encontrar

a) ‹u, v›=‹v, u› b) ‹u+ v, w › = ‹u, w› + ‹ v, w› c) ‹k u, v›=‹u, k v › = k ‹u, v›

2.- Calcular ‹u, v›

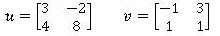
Propiedades del producto interior

1.- ‹0, v› = ‹v, 0›=0

2.- ‹u+ v, w › = ‹u, w› + ‹ v, w›

3.- ‹k u, v›=‹u, k v› = k ‹u, v›

4.- ‹u- v, w › = ‹u, w› - ‹ v, w›

5.- ‹u, v- w › = ‹u, v› + ‹u, w›

Norma de un vector

Si v es un espacio vectorial con producto interior, entonces la norma (o longitud) de un vector ║u║ en V se denota por y y se define como:

u= (u₁ ,u₂,….u_n)

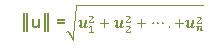
Comparando las fórmulas

‹u, v›= u₁ v₁ +u₂ v₂+…..+u_n v_n

Se puede concluir que

║u║=‹u, u›^1/2

Ejemplo

U=(1,2)

Si u y v son vectores en un espacio en V y k un escalar

1.- ║u║≥0

2.- ║u║= 0 si y solo si u=0

3. -║k u║ = 1k1 ║u║

4.- ║u+ v║≤║u║+║v║ desigualdad del triángulo

Distancia entre dos vectores

Se define como

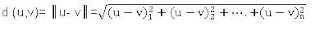
Ejemplo

U=(1,2) V=(0,3)

Propiedades

1.- d (u,v)≥0

2.- d (u,v)= 0 si y solo si u=v

3.- d (u,v)= d (v,u)

De acuerdo a lo antes expuesto

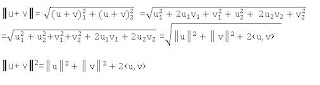
Ejercicios

1.- Hallar el valor de la norma de los siguientes vectores

U = (-1,2) p=-2+3x+2x ²

2.- Hallar la distancia entre los vectores

U=(-1,3) v=(3,0)

P=3+3x q= 2+4x-x²

3.- Suponer que u, v y w son vectores tales que;

‹u, v›=2 ‹u, w›= 5 ‹w, v›= -3 ║u║= 1 ║v║=2 ║w║=7

Hallar

‹u+ v, v + w› ‹2v-w, v-u›

║u+ v║ ║2w- v║ ║2u+ v-w║