Rango y Nulidad de una Matriz
La dimensión común del espacio renglón y del espacio columna de una matriz A se denomina rango y se denota rango (A), la dimensión del espacio nulo de A se llama nulidad y se denota nulidad (A).
Propiedad
Rango (A)= Rango (AT)
Teorema de la dimensión
Si es una matriz A con n columnas, entonces:
Rango (A) + nulidad (A) = n
El procedimiento para calcular el rango de una matriz es el siguiente
Se utiliza los procesos elementales por filas para transformar A en una matriz B en forma escalonada.
El rango de A es igual al número de filas no nulas (aquellas que se lograron escalonar).
Ejemplo
Sea A. determinar su rango y nulidad

Por procesos elementales
–f1+f2→f2 ^ –f1+f3→f3 f2+f3→f3
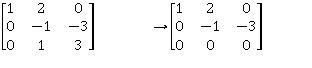
Ejercicios
Calcule el rango y la nulidad de A

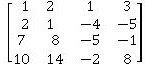
En cada caso usa la información que proporciona la tabla para encontrar la nulidad de Ay AT
a | b | c | d | e | f | g | |
Tamaño de A | 3x3 | 3x3 | 3x3 | 5x9 | 9x5 | 4x4 | 6x2 |
Rgo A | 3 | 2 | 1 | 2 | 2 | 0 | 2 |
No hay comentarios:
Publicar un comentario