Algebra de Matrices

Algebra de Matrices

Suma de Matrices

Dadas dos matrices de la mismo orden, A=(a_ij) y B=(b_ij), se define la matriz suma como: A+B=(a_ij+b_ij). Es decir, aquella matriz cuyos elementos se obtienen: sumando los elementos de las dos matrices que ocupan la misma posición.

Propiedades de la suma de matrices

Interna:

La suma de dos matrices de orden m x n es otra matriz dimensión m x n.

Asociativa:

A + (B + C) = (A + B) + C

Elemento neutro:

A + 0 = A

Donde O es la matriz nula de la misma dimensión que la matriz A.

Elemento opuesto:

A + (-A) = O

La matriz opuesta es aquella en que todos los elementos están cambiados de signo.

Conmutativa:

A + B = B + A

Video de explicación de esta operación

Matriz traspuesta

Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas

(A^t)^t = A

(A + B)^t = A^t + B^t

(α ·A)^t = α· A^t

(A · B)^t = B^t · A^t

Producto de un escalar por una matriz

Dada una matriz A=(a_ij) y un número real kR, se define el producto de un número real por una matriz: a la matriz del mismo orden que A, en la que cada elemento está multiplicado por k.

kA=(k a_ij)

Propiedades

Asociativa

a · (b · A) = (a · b) · A A M_mxn, a, b son constantes

Distributiva

a · (A+B) = a · A + a · B A,B M_mxn , a

(a+b) · A = a · A+b · A A M_mxn , a, b

Elemento Neutro

1 · A = A A M_mxn

Traspuesta

(aA)^t = a A^t

Video de explicación

Video 2

Producto de matrices

Dos matrices A y B se dicen multiplicables si el número de columnas de A coincide con el número de filas de B.

M_{m x n} x M_{n x p} = M _{m x p}

El elemento c_ij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos.

Propiedades del producto de matrices

Asociativa:

A · (B · C) = (A · B) · C

Elemento neutro:

A · I = A

Donde I es la matriz identidad del mismo orden que la matriz A.

No es Conmutativa:

A · B ≠ B · A

Distributiva del producto respecto de la suma:

A · (B + C) = A · B + A · C

Matriz inversa

A · A^-1 = A^-1 · A = I

Propiedades

(A · B)^-1 = B^-1 · A^-1

(A^-1)^-1 = A

(k · A)^-1 = k^-1 · A^-1

(A ^t)^-1 = (A ^-1)^t

Video de explicación

Cálculo por el método de Gauss

Sea A una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos como A^-1, seguiremos los siguientes pasos:

1º Construir una matriz del tipo M = (A I), es decir, A está en la mitad izquierda de M y la matriz identidad I en la derecha.

Considerando una matriz 3x3 arbitraria

Se amplía con la matriz identidad de orden 3.

2º
Utilizando el método Gauss se transforma la mitad izquierda, A, en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa: A^-1.

F₂ - F₁

F₃ + F₂

F₂ - F₃

F₁ + F₂

(-1) F₂

La
matriz
inversa
es:

Otro ejemplo

Video de explicación

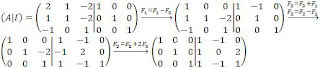
Forma matricial de un sistema lineal de ecuaciones

Un sistema lineal de m ecuaciones con n incógnitas es un sistema de la forma

ç

Donde:

A= es la matriz de coeficientes del sistema.
X= es la matriz de incógnitas.
B= es la matriz de términos independientes.
Luego un sistema lineal de ecuaciones se puede expresar matricialmente como A·X=B
Si la matriz de coeficientes es invertible, es decir, posee inversa entonces el sistema tiene solución A·X=B => A^-1·A·X=A^-1·B => X=A^-1·B·.
Por tanto resolver un sistema de ecuaciones a través de matrices consiste en poner el sistema en forma matricial. La solución, si la hay, será el producto de la inversa de la matriz de coeficiente (A^-1) por la matriz de términos independientes (B)

.Video de explicación por Gauss Jordan

Ejercicios

Encontrar la inversa de las siguientes matrices

Si

Despeje x de Ax=b si

Traza de una Matriz

La traza de una matriz cuadrada A de n x n está definida como la suma de los elementos de la diagonal principal de A.

Es decir,

donde aij representa el elemento que está en la fila i ésima y en la columna j ésima de A

Propiedades

Potencia de Matrices

Consiste en multiplicar tantas veces la matriz como lo indica el exponente.

A = ( 1 -2 ) 5 3

A . A = A2 = ( -9 -8 ) 20 -1

Propiedades

Regla de Cramer

Regla de Cramer

Los pasos a seguir para calcular los sistemas de ecuaciones según la regla de Cramer son los siguientes:

1. Hallar la matriz ampliada (A b) asociada al sistema de ecuaciones, esto es: que la primera columna esté formada por las entradas de los coeficientes de la primera incógnita de las ecuaciones; que la segunda columna la formen las de la segunda incógnita, y así hasta llegar a la última columna, que estará constituida por las entradas de los términos independientes de las ecuaciones.

2. Calcular el determinante de A. Proseguir solo si el determinante de A es distinto de cero. El hecho de que este sea igual a 0 indica que dos filas o columnas son combinaciones lineales entre si y este método no sería el indicado.

3. Aplicar la regla de Cramer, que consiste en:

a) ir sustituyendo la primera columna del det (A) por los términos independientes;

b) dividir el resultado de este determinante entre el det (A) para hallar el valor de la primera incógnita;

c) continuar sustituyendo los términos independientes en las distintas columnas para hallar el resto de las incógnitas.

Ejemplo:

Sea el sistema de ecuaciones lineales formado por dos ecuaciones con dos incógnitas:
3x - 2y =1
x +5y = 3

Encontrar el valor de x e y mediante la regla de Cramer.

Empezaremos con el primer paso, que consiste en hallar la matriz ampliada A b asociada al sistema de ecuaciones lineales:
x y



El segundo paso es calcular el determinante de A. Así pues:
|A|= 3.5- (-2. 1)= 15 +2=17

Y el tercero y último paso consiste en calcular las incógnitas:
|B|= 1.5- (-2.3)= 11

|C|= 3.3 -1.1 = 9 -1 = 8


Solución trivial (11/17,8/17)
Ejercicios para resolver por la Regla de Cramer
1.-" -2x+3y-z=1"
"X+2y-z=4"
" -2x-y+z=-3"


2. "2x+4y+6z=2"
x+2z=0
2x+3y-z=-5"

Determinantes

EL DETERMINANTE

El determinante es una función que le asigna a una matriz de orden n (cuadrada), un único número real llamado el determinante de la matriz. Si A es una matriz de orden n, el determinante de la matriz A lo denotaremos por det(A) o también por A( las barras no significan valor absoluto). El cálculo se realiza con la permutación de los elementos de la matriz sin repetir filas ni columnas, el signo que se le asigna es por ser par o impar de acuerdo a la ubicación del número según la columna que ocupan

Determinante de una matriz de orden 1
Si A es una matriz de orden uno, entonces det(A)=a.

, entonces det(A)=-2 o

,Sientonces det(A)=0 o

Si entonces det(A)=2 o

Menor de una matriz de orden n
Sea A una matriz de orden , se define como el menor M_ij asociado al elemento a_ij de A como el determinante de la matriz que se obtiene al eliminar la fila i y la columna j de la matriz A.

Sea
	el menor asociado a a11.
	el menor asociado a a12.
	el menor asociado a a21.
	el menor asociado a a22.

Cofactor de una Matriz de orden n

El cofactor c_ij asociado al elemento a_ij de A esta dado por c_ij = (-1)^{i +j} │M_ij│ .

	El cofactor asociado al elemento a11.
	El cofactor asociado al elemento a12.
	El cofactor asociado al elemento a21.
	El cofactor asociado al elemento a22.

Determinante de una matriz de orden superior (Método de Lagrange)
Si A es una matriz de orden entonces el determinante de la matriz A es la suma de los elementos de cualquiera de las filas o columnas de A multiplicados por sus respectivos cofactores.

.
Hallar el determinante de la matriz

Previamente se había calculados los cofactores. Este cálculo se realizó con la primera fila

Comprobando que se puede aplicar con cualquier columna a continuación se realizara con la segunda.

│A│= a₁₂ c₁₂ + a₂₂ c₂₂= (-1)(-3) +(1)(2)= 3+2= 5

Se demuestra de esta forma que el resultado del determinante no varía por la selección de una fila o una columna.

Sea

Para determinantes de orden 2 se realiza como regla mnemotécnica la multiplicación en cruz de los elementos. Si se aprecia la permutación de los elementos sin repetir filas ni columnas. Se llega esta fórmula

Calcular el determinante de la matriz

Hallar el determinante de la matriz de orden 3

Solución
Para encontrar el menor se elimina el primer renglón y la primera columna de A y se calcula el determinante de la matriz resultante.

De manera similar, para encontrar el menor, se elimina el primer renglón y la segunda columna de A0 y se calcula el determinante de la matriz resultante.

Para encontrar el menor, se elimina el primer renglón y la tercera columna de A

los cofactores son

el determinante de la matriz A se calcula así

video 1

video 2

Regla de Sarrus

Paso 1 Escriba la matriz A y enseguida las primeras dos columnas de A como se muestra a continuación

a₁₁ a₁₂ a₁₃ │a₁₁ a₁₂

a₂₁ a₂₂ a_23│ a₂₁ a₂₂

a₃₁ a₃₂ a_33│ a₃₁ a₃₂

Paso 2 Calcule los productos indicados por los diferentes colores las flechas (que a continuación se indican). Los productos correspondientes a las flechas que se dirigen hacia abajo se toman con signo positivo, mientras los productos correspondientes a las flechas que se dirigen hacia arriba se toman con signo negativo.

+ + + - - -

Paso 3 Sume los productos con los signos adecuados según se determinó en el paso 2

Calcular el determinante de la matriz A del ejemplo 2.5 usando la regla de Sarrus.

Paso 1

Paso 2

Paso 3

OBSERVACIÓN
La regla de Sarrus únicamente se puede utilizar para determinantes de orden 3.
video de explicación
Teorema

Sea A una matriz de orden n, entonces el determinante de A esta dado por

	Desarrollo del i-ésimo renglón
o tal vez
	Desarrollo del j-ésima columna

PROPIEDADES DE LOS DETERMINANTES

1.A^t= A

El determinante de una matriz A y el de su traspuesta A^t son iguales.

2. A=0 Si:

Posee dos filas y columnas iguales

Todos los elementos de una fila y columna son nulos.

Los elementos de una línea son combinación lineal de las otras.

F₃ = F₁ + F₂

3. Un determinante triangular es igual al producto de los elementos de la diagonal principal..

4. Si en un determinante se cambian entre sí dos líneas paralelas su determinante cambia de signo.

5. Si a los elementos de una línea se le suman los elementos de otra paralela multiplicados previamente por un nº real el valor del determinante no varía.

6. Si se multiplica un determinante por un número real, queda multiplicado por dicho número cualquier línea, pero sólo una.

7. Si todos los elementos de una fila o columna están formados por dos sumandos, dicho determinante se descompone en la suma de dos determinantes.

8. A·B =A·B

El determinante de un producto es igual al producto de los determinantes.

video de explicación

Cálculo de un determinante de cualquier orden

Consiste en conseguir que una de las líneas del determinante esté formada por elementos nulos, menos uno: el elemento base o pivote, que valdrá 1 ó -1.

los siguientes pasos:

1.Si algún elemento del determinante vale la unidad, se elige una de las dos líneas: la fila o la columna, que contienen a dicho elemento (se debe escoger aquella que contenga el mayor número posible de elementos nulos).

2.En caso negativo:

1. Nos fijamos en una línea que contenga el mayor número posible de elementos nulos y operaremos para que uno de los elementos de esa línea sea un 1 ó -1 (operando con alguna línea paralela).

2.Dividiendo la línea por uno de sus elementos, por lo cual deberíamos multiplicar el determinante por dicho elemento para que su valor no varie. Es decir sacamos factor común en una línea de uno de sus elementos.

3.Tomando como referencia el elemento base, operaremos de modo que todos los elementos de la fila o columna, donde se encuentre, sean ceros.

4. Tomamos el adjunto del elemento base, con lo que obtenemos un determinante de orden inferior en una unidad al original.

= 2(-58)

video de explicación